Fondamenti del Deep Learning
Che cos'è il deep learning? Quali sono i suoi principi di funzionamento?
Iniziamo con un gioco: un giocatore (pilotato dal computer) deve prendere i pallini rossi ed
evitare quelli verdi per vedere il proprio punteggio aumentare (il grafico sulla destra).
GIOCATORE 1
GIOCATORE 2
Riuscite a capire quale dei due giocatori sia il più bravo? Questa è la magia del deep learning: il secondo giocatore è stato "allenato" e quindi sa come comportarsi per aumentare il proprio punteggio. Mentre leggete continueranno a giocare e quindi potrete vedere il grafico del punteggio per ognuno dei due. Consiglio infatti di tornare a vedere i grafici più tardi, quando avranno una forma su cui si può trarre qualche conclusione.
Per capire cosa sia il deep learning bisogna intanto comprendere cosa vi sia alla base del suo processo di allenamento. L'unità base è il neurone, una struttura che prende in ingresso uno o più input, li processa usando una funzione matematica e restituisce quindi l'output in base ai calcoli svolti.
Esistono diversi tipi di neuroni: il primo ad essere utilizzato è stato il perceptron, un neurone che prende in ingresso una serie di input pesati (vengono cioè moltiplicati per un peso), li somma, aggiunge una costante (chiamata bias), applica una funzione e, in base al risultato, restituisce uno 0 o un 1.
Si sono quindi messi insieme diversi perceptron per formare una rete neurale in grado di svolgere compiti più complessi di un singolo neurone da solo. Queste reti non hanno tuttavia un'architettura complessa: assumono infatti una struttura stratificata, in cui un neurone di uno strato riceve come input gli output dei neuroni dello strato precedente e fornisce il proprio output ad ognuno dei neuroni dello strato successivo, che lo accetta come input pesato.
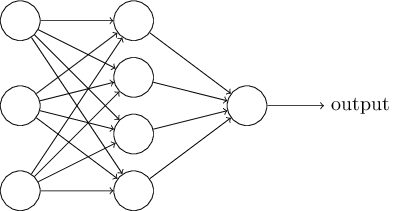
La struttura di una semplice rete neurale a tre strati con: 3 neuroni di input, 4 neuroni nascosti e un solo neurone di output.
Il primo strato viene sempre detto input layer e raccoglie tutti i neuroni che fungono da input per la rete. Tali neuroni non ricevono alcun input e il loro output è equivalente ai dati in ingresso alla rete. Servono solo come segnaposto, per indicare in modo omogeneo anche gli input della rete.
L'ultimo strato prende il nome di output layer: i risultati in uscita da ciascun neurone di questo strato costituiscono l'output complessivo della rete. Infatti una rete neurale può avere anche più di un output (avrà tanti output quanti sono i neuroni nell'output layer).
Ognuno degli strati intermedi è denominato hidden layer, chiamato in questo modo perché risulta appunto "nascosto" (non è né di input né di output). Mentre possono esservi un solo input layer ed un unico output layer, una rete può avere anche più di un solo hidden layer. Una rete con molti strati riuscirà quindi a compiere astrazioni sempre migliori man mano che si procede dall'ingresso all'uscita.
Ad esempio, una rete che debba riconoscere delle immagini avrà un neurone di input per ogni pixel dell'immagine (supponiamo che l'immagine sia in bianco e nero), un primo hidden layer che si occuperà di riconoscere figure elementari (un cerchio, un quadrato...), un secondo strato intermedio che studierà figure un po' più complesse (un cerchio con al suo interno altri cerchi...) e così via, fino all'output layer. Ovviamente questa è una semplificazione di come funzionano le reti neurali, anche se concettualmente il loro funzionamento è questo.
Finora abbiamo parlato di reti di perceptron. Ben presto però, si scoprì che questo tipo di neuroni era fin troppo limitato: un output di soli zero e uno non soddisfaceva le esigenze dei ricercatori. Così si passò ad utilizzare il neurone sigmoide. Questo tipo di neurone, a differenza del perceptron, non solo può accettare come input qualsiasi valore reale, ma può fornire come output un valore reale compreso tra 0 e 1. Il loro uso, tuttavia, non differisce da quelli dei perceptron: tutto quello che abbiamo detto finora sulle reti neurali è ancora valido anche per i neuroni sigmoidi.
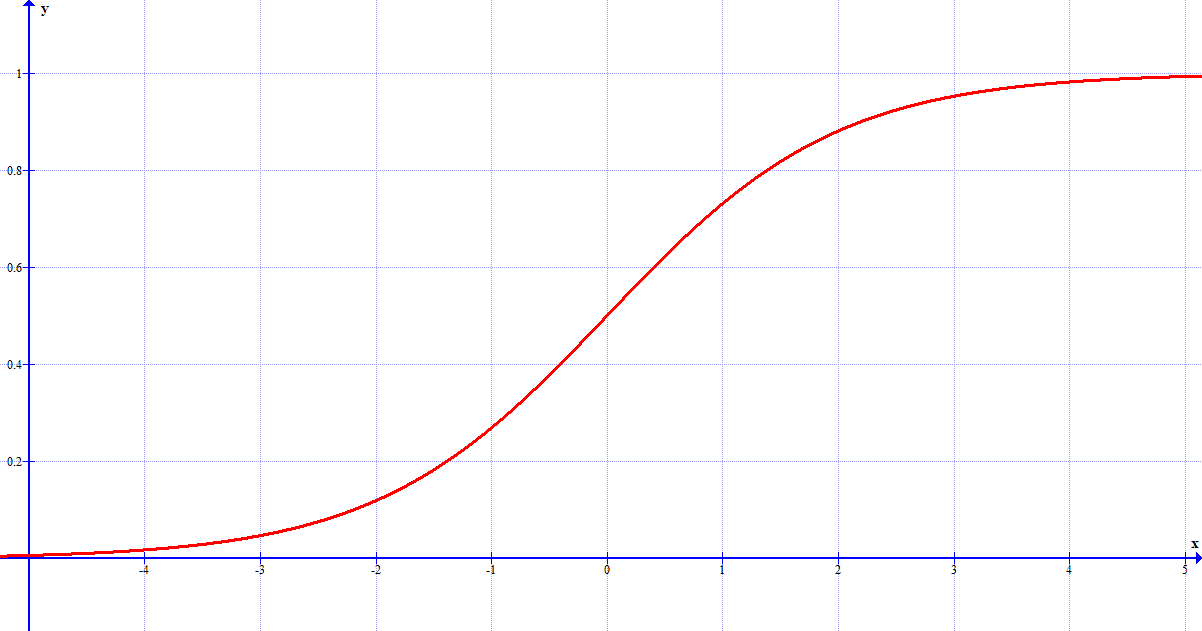
Il grafico della funzione sigma, dal cui nome deriva la denominazione dei neuroni sigmoidi. Viene utilizzata per calcolare l'output di questo tipo di neuroni.
I neuroni da soli non riescono ovviamente ad imparare. Per fare in modo che una rete neurale possa imparare si deve fare in modo di cambiare in modo appropriato i pesi dei collegamenti tra i neuroni e i bias, le costanti tipiche di ciascun neurone. Sono i valori di questi parametri che differenziano le reti neurali dei due giocatori dell'esempio iniziale, in quanto la loro struttura è identica.
Ma come possiamo identificare i valori corretti? Dietro tutto il procedimento vi è ovviamente una serie di calcoli che tralascio in questa sede. Tuttavia, voglio farvi capire come funziona.
Per sistemare i valori di tutti i parametri viene usata una funzione detta di costo, che misura quanto la rete si sta comportando bene. Il nostro obiettivo è trovare il valore di uscita della rete che minimizza tale funzione. Tuttavia, farlo in maniera analitica, svolgendo ovvero tutti i calcoli esatti, risulterebbe troppo pesante, in quanto i parametri di cui dovremmo tenere conto sono davvero tanti (con un bias per ogni neurone e con un peso per ogni collegamento tra neuroni si arriva tranquillamente a qualche migliaia di parametri!). L'algoritmo che si segue è chiamato algoritmo del gradiente decrescente. Ve lo spiego ricorrendo ad un esempio.
Immaginiamo di avere una pallina da golf, che rappresenta il risultato corrente della rete neurale. La buca è il risultato corretto, quello che vorremmo che la nostra rete avesse. Quanto più la pallina è vicina alla buca, tanto più il risultato è corretto (e la funzione costo bassa). Il nostro obiettivo è ovviamente fare buca. Per prima cosa, calcoliamo il gradiente, che ci dice la direzione in cui dovremo tirare la pallina. Una volta calcolato è il momento di tirare. Noi siamo tipi pazienti e non badiamo al numero di tiri che dovremo fare: procediamo per tiri di piccola potenza nella direzione che abbiamo stabilito. Ci avviciniamo pian piano alla buca. Vi è un parametro che misura la potenza dei nostri tiri: è il tasso di apprendimento (spesso indicato con la lettera greca η). Anche per il tasso di apprendimento ci vuole tuttavia il giusto valore. Troppo basso e dovremo rimanere ore per mandare la pallina in buca. Troppo alto e la nostra pallina sorpasserà la buca, allontanandoci dal nostro obiettivo. Ripetendo quindi la sequenza calcolo del gradiente - tiro della pallina ci avvicineremo sempre di più alla buca, finché non la raggiungiamo (e avremo trovato quindi il minimo della funzione costo!). Il procedimento concettuale è quindi questo.
Nella pratica, per allenare la rete si prende una serie di input di allenamento di cui si conosce il valore corretto di output e si dà in pasto alla rete per osservarne il risultato. Si procede quindi come descritto sopra, calcolando il gradiente del costo e aggiustando ciascuno dei parametri (pesi e bias) per muoverci verso il minimo della funzione costo. Calcolare però il gradiente su ognuno dei possibili input è molto dispendioso. Si procede quindi a calcolare il gradiente su un gruppo di input di allenamento scelti casualmente detto mini-batch. Quindi: scegliamo un mini-batch, alleniamo la rete con quello, scegliamo un altro mini-batch, la alleniamo... e così via, finché non finiamo una cosiddetta epoca di allenamento, ovvero finiamo di passare tutti gli input. Poi si ricomincia una nuova epoca e si ripete fino a quando non si ritenga che la rete sia pronta.
Le basi per capire un po' come funziona il deep learning sono finite! Potete passare a vedere gli esempi disponibili, provando magari a cambiare anche i parametri di cui abbiamo parlato per vedere che risultati si ottengono!
Per finire, tornando ai nostri due giocatori, si può vedere come il secondo giocatore abbia mantenuto un punteggio molto più alto e con oscillazioni meno ampie del primo. Il procedimento con cui si è allenato il secondo giocatore non è dissimile a quello che abbiamo appena visto: ha scoperto che prendere le palline rosse lo avvicinava alla buca e perciò ha sistemato i propri parametri per cercare di evitare le verdi e mangiare le rosse.