Difficoltà di allenamento
Possiamo costruire reti neurali di qualsiasi complessità: dalle più semplici, composte da un solo hidden layer e con pochi neuroni, alle più complesse, con decine di neuroni nascosti. Ovviamente, sono le reti complesse che sono in grado di eseguire i compiti più complicati e sono perciò loro oggetto di studio. Infatti, più hidden layer possono creare diversi livelli di astrazione.
Tuttavia, quando si è provato ad allenare reti complesse si è notato un problema non indifferente: i diversi strati di neuroni in una rete complessa imparano a velocità ampiamente diverse. In particolare, quando gli ultimi layer si stanno allenando bene, i primi faticano a migliorare (o viceversa). Insomma, la rete neurale non sta imparando in maniera uniforme. Sembra vi sia una instabilità intrinseca associata all'apprendimento delle reti neurali complesse che usano l'algoritmo del gradiente decrescente.
Se analizziamo la velocità di cambiamento di pesi e bias all'interno di una rete neurale con due strati, ad esempio, non ci sorprende vedere velocità diverse, in quanto questi parametri sono inizializzati in maniera casuale. Tuttavia, ci si è accorti che i neuroni del secondo layer imparano più velocemente dei neuroni nel primo strato della rete.
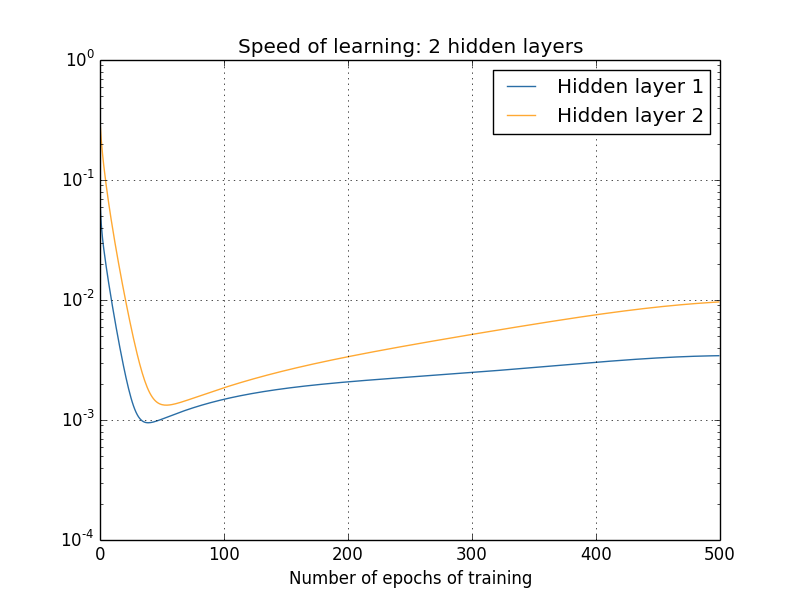
La velocità di apprendimento dei due layer: si può vedere come il primo sia più lento del secondo.
Inoltre, se si aggiungono layer, tale schema si ripresenta, causando un allenamento più veloce in fondo alla rete che non all'inizio. Questo fenomeno prende il nome di problema del gradiente evanescente. L'alternativa non è migliore: fare in modo che siano i primi layer ad imparare più velocemente rallenta quelli successivi (problema del gradiente divergente).
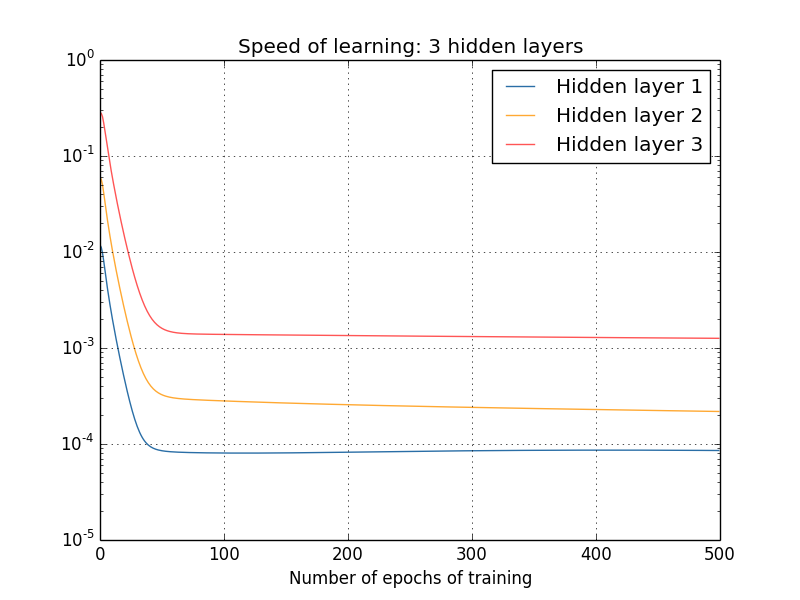
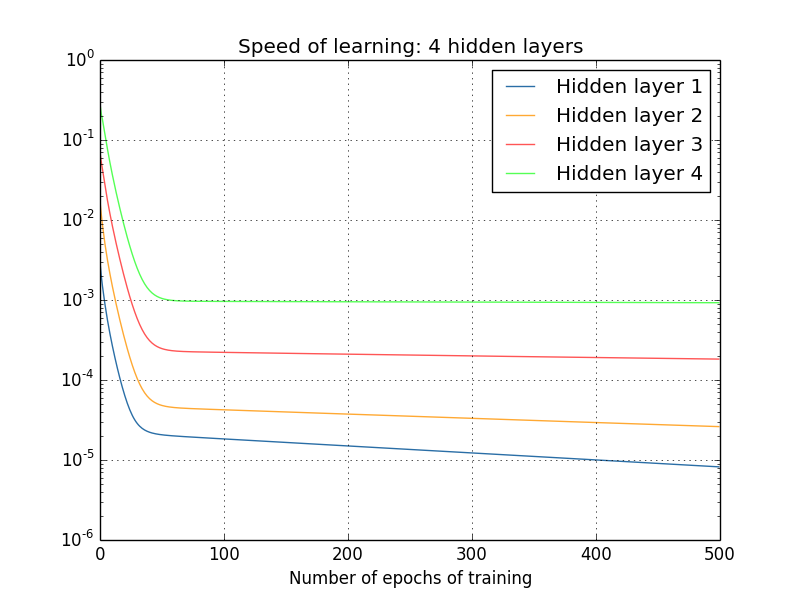
Anche aggiungendo livelli alla rete il problema non si risolve, anzi la differenza tra il primo e l'ultimo layer si fa sempre più evidente.
Più in generale, quindi, il gradiente (che stabilisce la velocità di apprendimento della rete) è instabile e tende o a diventare eccessivamente piccolo o troppo grande.
Ma cosa lo causa esattamente? Tralasciando i calcoli, il problema è insito nell'algoritmo che usiamo, che sfrutta una serie di prodotti, in cui però gli elementi sono minori di 1. Poiché questi prodotti coinvolgono sempre più elementi man mano che torniamo nei primi layer, il gradiente si abbassa sempre di più e i neuroni imparano sempre più lentamente.
Se modifichiamo i parametri in modo che essi siano maggiori di 1, otterremo l'effetto inverso e cadremo nel problema divergente. Il problema fondamentale è comunque l'instabilità della situazione. Infatti, le reti più complesse soffrono il problema del gradiente instabile.
Si sta studiando molto il problema e le sue causa e non è ancora stata trovata una soluzione sistematica e ben definita, bensì si procede caso per caso, basandosi sulle prestazioni che ottengono le nostre idee.